Decision Trees Classifier
Tree-based models are a type of machine learning technique that uses a tree- like structures to make predictions. The most basic type of a tree-based model is a Decision Tree. A Decision Tree guides observation through a tree-like structure with many branches. Below is an example of a simple tree model, that predicts the type of Vehicle based on some set of features.
Sample Decision Tree
Figure is taken from Machine Learning with R, Tidyverse and MLR -Textbook
Some important terminology here:
- Root Node: The root node is the parent node that determines the partition of the rest of the tree. It contains all data prior to splitting.
- Decision Nodes: The decision nodes are subsequent nodes that further split the data into either decision nodes or leaf nodes.
- Leaf Nodes: Leaf nodes are the end point of the tree, they house the class/label of the observations.
Instinctively, we may wish to ask, given the knowledge of the nature of a decision tree, how it is that the algorithm we choose to use will decide how the tree is formed. In particular, there are three questions to consider:
- What variable makes the best root node?
- Which variables make the best decision nodes?
- In what order should these decision nodes be?
Entropy and Theory of Information
Entropy is a concept commonly linked to physics and mathematics that concerns with the measure of chaos in a system. To reduce it to our use in data analytics and machine learning, entropy is a technique that attempts to measure impurity present within a particular data set. In order words, we can use it to measure how homogeneous our data set is. This is useful because as we seek to classify objects, we wish to reduce impurity, or phrased differently, maximize homogeneity.
Formally, Entropy of a variable can be calculated using the following formula:
$$ (Shannon's)Entropy = H(Y, X) = - \sum_{i=1}^{m} p_i * log_2(p_i) $$
where
$Y$: categorical dependent variable
$X_k$: Set of predictor variables with $k$ distinct values.
$p$ is the probability of a certain category $m$ in $Y$.
Entropy Example for the Binary Case
Let's look at an example of the Binary case, where the labels belong to two classes only. The code below will evaluate the entropy against different composition of the labels. For simplicity, let's say, if there are labels $A$ and $B$, we will generate different proportions for A and B will equal to $1-p(A)$.
The general formula for Entropy for Binary case is then:
$$ Entropy = - p(A) * log_2(P(A)) - (1 - P(A)) * log2(1 - p(A)) = -plog_2(p) - (1 - p)log_2(1 - p) $$
# Define the entropy function for a binary system
entropy_binary <- function(p, base = 2) {
# Ensure probabilities are within (0,1) to avoid log(0)
p <- ifelse(p == 0, .Machine$double.eps, ifelse(p == 1, 1 - .Machine$double.eps, p))
q <- 1 - p
# Compute the entropy
H <- - (p * log(p, base = base) + q * log(q, base = base))
return(H)
}
# Create a sequence of probability values from 0 to 1
p_values <- seq(0, 1, length.out = 1000)
# Calculate entropy for each probability
H_values <- entropy_binary(p_values)
# Plot the entropy as a function of probability
plot(p_values, H_values, type = 'l', lwd = 2, col = 'blue',
xlab = 'Probability (p)',
ylab = 'Entropy H(p) [bits]',
main = 'Entropy of a Binary System')
# Add grid lines for better visualization
grid()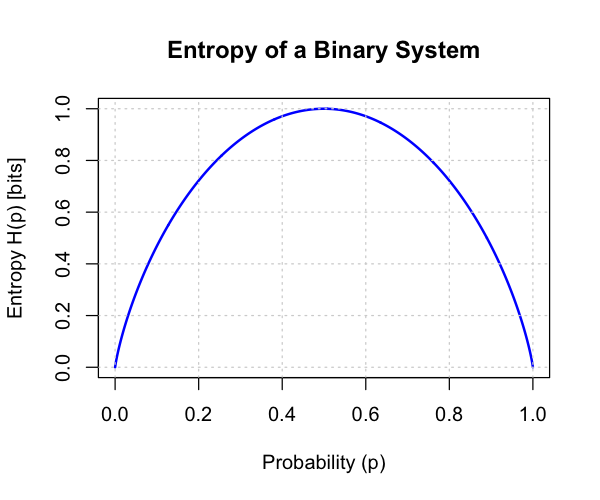
Think through the interpretation of the Curve above. Specifically, Entropy of a system when the probabilities of $A$ and $B$ are at .5. That is, at the highest randomness, the entropy is high. As the probability of an individual label becomes higher than the other, the entropy reduces.
How to Pick Nodes - Expected Entropy and Information Gain
The entropy calculation gives us everything we need to be able to select nodes for splits. Naturally, with a few modifications, we can apply entropy to develop a more useful measure that tells us exactly how much impurity we would reduce by selecting a specific node. To do this we need two more modified versions of entropy:
1.1. Expected Entropy
The first idea is the expected Entropy. The Expected Entropy provides an estimated entropy value when a particular variable is selected. It does this by computing the Expected Entropy of the child nodes given the probabilities of their categories. Mathematically, the formula is:
Suppose an Attribute $A$ with $k$ distinct values is selected as a node, to get the expected entropy, we compute the following:
$$ EH(A) = \sum_{i=1}^{k} \frac {p_i + n_i} {p + n} H(\frac {p_i}{p_i + n_i}, \frac{n_i}{p_i + n_i} ) $$
Let us use an example to demonstrate the computation above:
Suppose we have 12 observations equally distributed of a label as to whether an individual will play a game based on weather (and other factors). On this example, we will use the weather as a node to compute the EH value.
$$ EH(Weather) = p_{rainy} * H(p_{rainy, play}, p_{rainy,not\ play}) + p_{sunny} * H(p_{sunny,play}, p_{sunny,not\ play}) + p_{cloudy} * H(p_{cloudy,play}, p_{cloudy,not\ play}) $$
To implement it directly, the EH(Weather) is given by:
$$ EH(Weather) = \frac {2}{12} * H(0, 1) + \frac {4}{12} * H(1, 0) + \frac {6}{12} * H(2/6, 4/6) = .4589 $$
1.2. Information Gain
In the above example, we have calculated Expected Entropy at a given column variable. In reality we will have to compute these for all variables. However this is till not sufficient, the final piece is to get the information gain which is the difference between entropy of the complete data set and the entropy at the variable.
$$IG = H(Y,X) - EH(A)$$
For our example above, this will correspond to:
$$ IG(weather) = 1 - EH(Weather) = 1 - .4589 = .541 $$
So by choosing the Weather variable, we have reduced the chaos, or gained information from 1 to .541. Typically we do this across all the variables and do it recursively until we have the tree.
# loading the necessary libraries
# keep in mind that some libraries need installing
library(ISLR)
library(ggthemr)
library(ggplot2)
library(tidyverse)
library(tidymodels)
library(rpart.plot)
library(gt)
# setting theme
ggthemr('pale')# reading the dataset into the variable
data("Carseats")
# show the sample of the dataset
car_seat_sales <- as_tibble(Carseats)
head(car_seat_sales)names(car_seat_sales)dim(car_seat_sales)Fitting a Classification Decision Tree
We begin by classifying the dataset using Sales as our dependent variables and other variables as predictors. As we have seen above, the sales data is in fact a numerical value. Therefore, we need to convert is to a factor variable.
# create a new column and remove the older sales
car_seat_sales <- car_seat_sales %>%
mutate( High = factor( if_else(Sales > 8, 'Yes', 'No'))) %>%
select(-Sales)Now, we can generate our train and test sets.
# setting seed for reproducibility
set.seed(3261)
data_split <- initial_split(car_seat_sales, prop = .8, strata = High)
train_data <- training(data_split)
test_data <- testing(data_split)
dim(train_data); dim(test_data)Decision Tree Model Setup
As we have seen a few times now with tidymodels, we will need to configure our model by setting up the engine and task definition to suit our specific needs.
# defining the model specification
decision_tree_classifier <- decision_tree( tree_depth = 6 ) %>%
set_engine('rpart') %>%
set_mode('classification')
# fitting the model
decision_tree_fit <- decision_tree_classifier %>% fit(High ~., data = train_data)
decision_tree_fitVisualizing the Tree
To visualize the decision tree notes, we need to extract the model fit from the engine and pass it to our rpart.plot which will render the tree. The visualization allows us to see the feature importance.
extract_fit_engine(decision_tree_fit) %>%
rpart.plot(roundint=FALSE)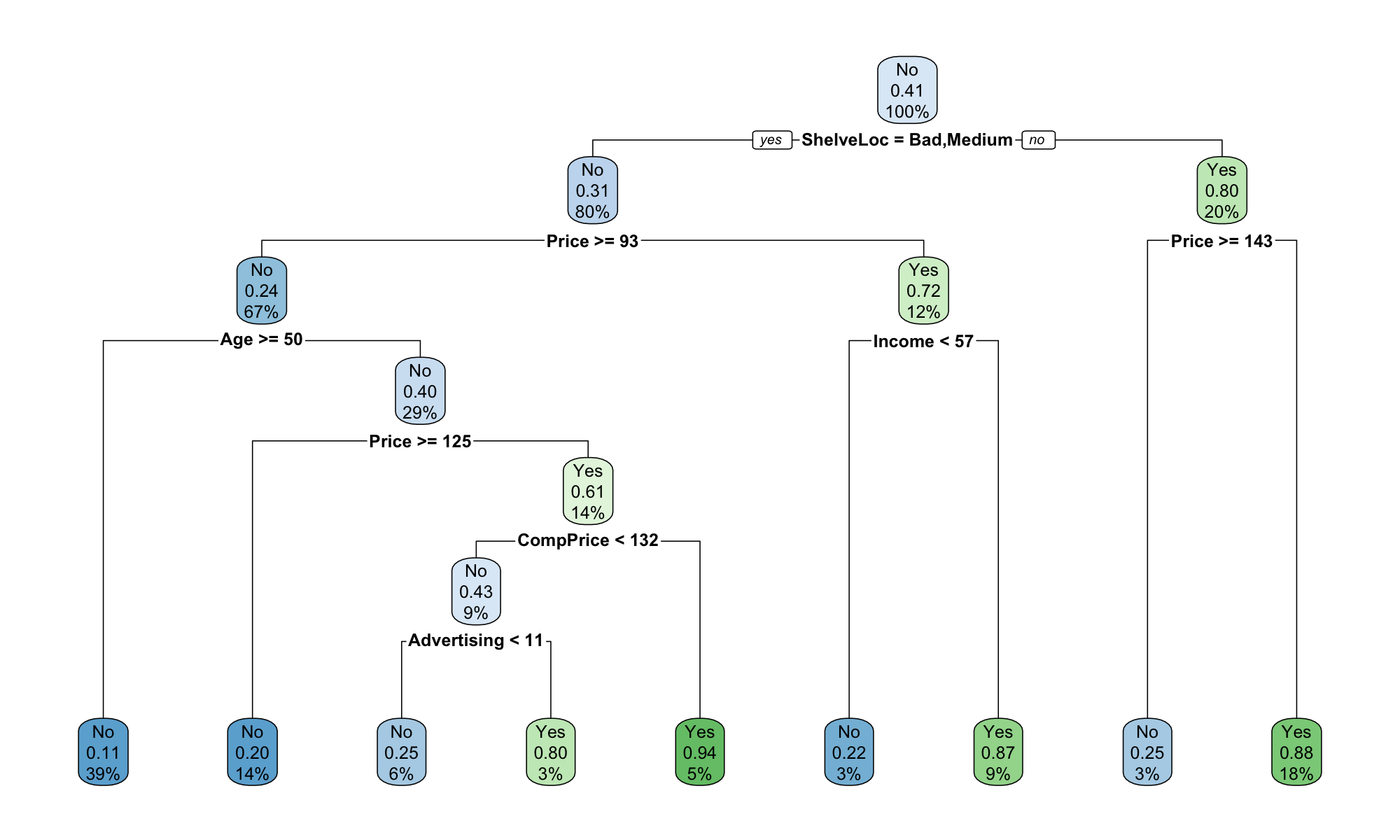
We see that the most important node for the sales is the Shelving location. In particular, let us note that the node differentiates between Good vs. Medium and Bad locations. It is also interesting to note that the price comes second to location.
Model Accuracy and Fit Assessment
Like with every other classification model, we can compute the accuracy and confusion matrix to further investigate the model performance. We do this with both the test and train sets.
# train dataset accuracy
augment( decision_tree_fit, new_data = train_data ) %>%
accuracy(truth = High, estimate = .pred_class)# Train Confusion Matrix
augment( decision_tree_fit, new_data = train_data ) %>%
conf_mat(truth = High, estimate = .pred_class)The training set accuracy is at 85%. Without any optimization parameters, this is a relatively good accuracy level.
# test dataset accuracy
augment( decision_tree_fit, new_data = test_data ) %>%
accuracy(truth = High, estimate = .pred_class)The test set accuracy is at ~76%, nearly ~10 percentage points lower than the training set.
Tuning the Complexity of a Decision Tree
The decision tree classifier developed above has not been tuned or cross-validated to determine the depth of the tree that is best performing. To do this, we implement a grid search on k_fold validation. The implementation below is an example of how to execute this.
#defining the model
decision_tree_classifier <- decision_tree() %>%
set_engine('rpart') %>%
set_mode('classification')
# classification workflow
decision_tree_class_workflow <- workflow() %>%
add_model( decision_tree_classifier %>%
set_args( cost_complexity = tune() ) ) %>% # tree_depth = tune()
add_formula(High ~.)
# defining cross validation and parameter grid
car_seats_kfold <- vfold_cv(train_data) # by defaults this is a 10 fold validation
# Generate 10 values from this grid in the range (-3, -1) = cost complexity: 1/(x + 1)
# (the relation of the cost complexity function works well with these values)
param_grid <- grid_regular( cost_complexity( range = c(-3, -1)), levels = 10 )
# tuning the model
tune_res <- tune_grid(
decision_tree_class_workflow,
resamples = car_seats_kfold,
grid = param_grid,
metrics = metric_set(accuracy)
)Visualizing Cost Complexity
The autoplot() function returns the Accuracy to Cost_Complexity parameter to help us best assess how the grid search performed. We can see that model 7 performed best yielding the highest accuracy.
autoplot(tune_res) + ggtitle('Cost Complexity Plot: Accuracy to Cost Complexity')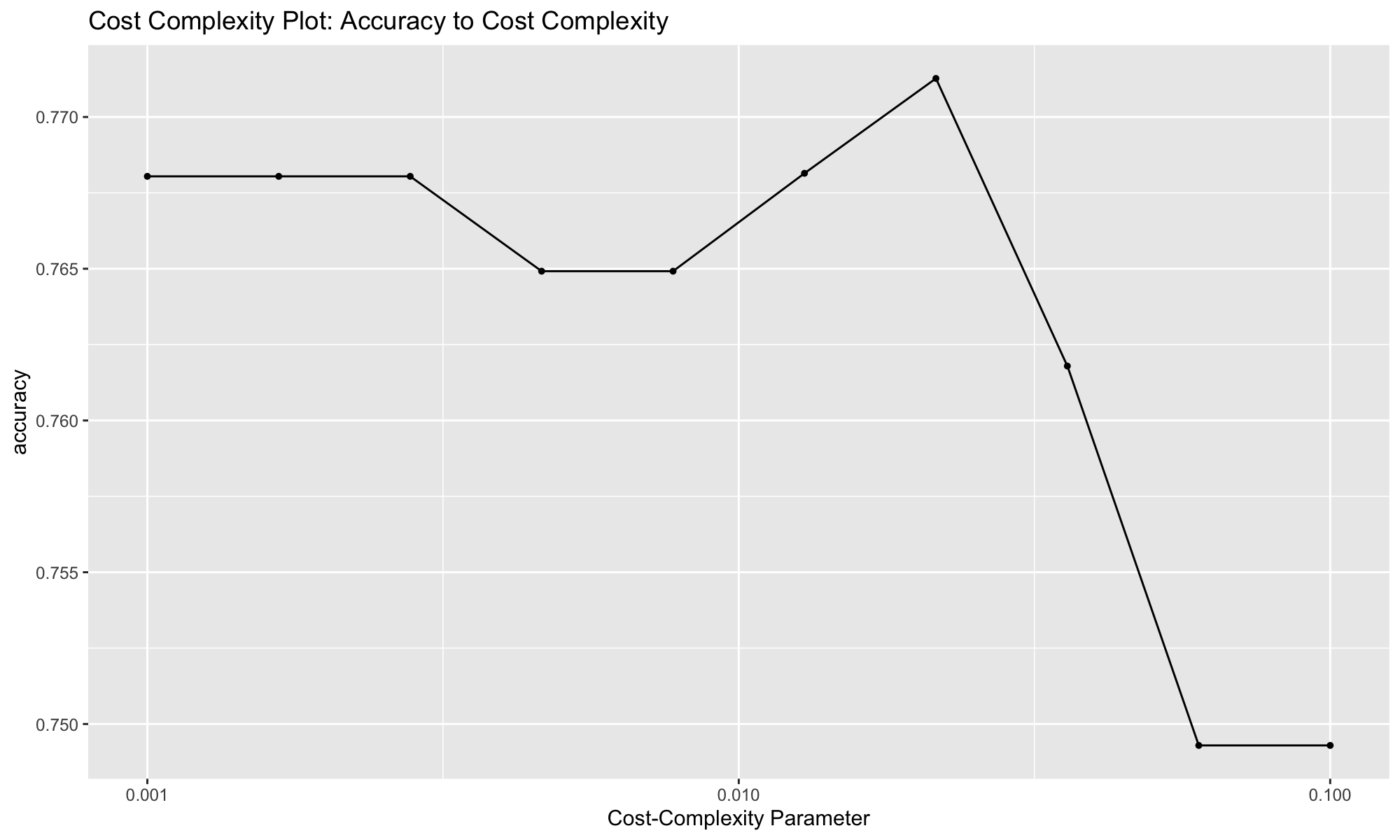
Extracting the Best Performing Model
From the visualization, we know that the best performing model based on accuracy is Model 7. We can now extract the model using the function select_subset.
best_complexity <- select_best(tune_res, metric = "accuracy")
best_complexityFitting the Best Model to the Full Train Data
With have performed cross validation to extract the best performing model.
# extracting the final classifier
decision_tree_final_classifier <- finalize_workflow( decision_tree_class_workflow, best_complexity )
# fitting it to the full train data
decision_tree_final_fit <- fit(decision_tree_final_classifier, data = train_data)
decision_tree_final_fitdecision_tree_final_fit %>%
extract_fit_engine() %>%
rpart.plot(roundint = FALSE)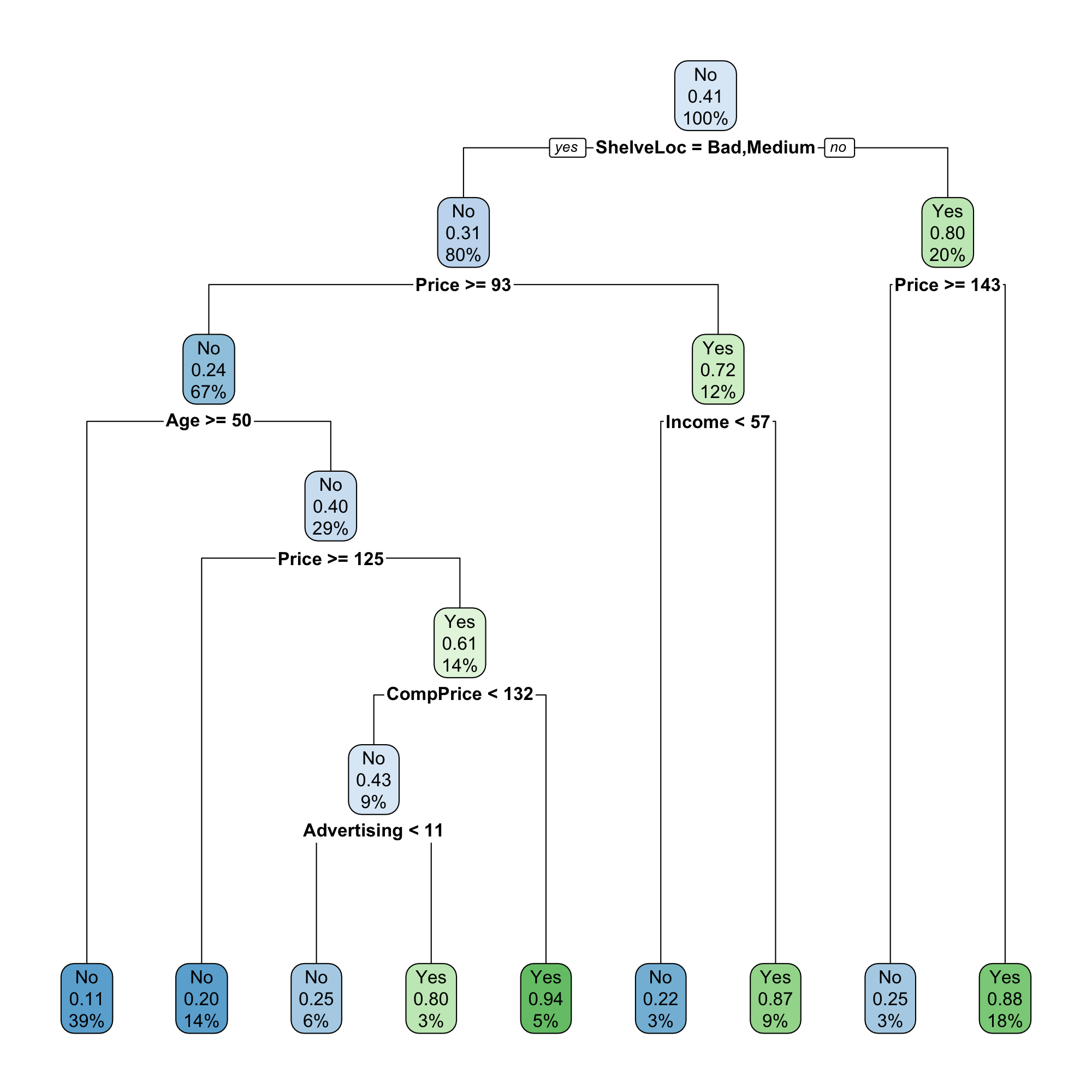
# train dataset accuracy
augment( decision_tree_final_fit, new_data = train_data ) %>%
accuracy(truth = High, estimate = .pred_class)# test dataset accuracy
augment( decision_tree_final_fit, new_data = test_data ) %>%
accuracy(truth = High, estimate = .pred_class)