Logistic Regression

Logistic regression is a statistical method used for binary classification problems, where the outcome variable has two possible categories. Unlike linear regression which predicts continuous values, logistic regression estimates the probability that an observation belongs to a particular class. It uses the logistic function to transform linear combinations of input features into probabilities between 0 and 1, making it particularly useful for predicting outcomes such as yes/no, pass/fail, or default/no default scenarios in financial modeling.

The Dataset

For this task, we will use the Default dataset from the ISLR (Introduction to Statistical Learning with R) book. This dataset contains information on whether an individual defaults on their credit card payment along with predictors such as income, balance, and student status. It is an excellent example for practicing logistic regression.

Metadata

default: Indicates whether the individual defaulted on their credit card payment, (Yes, No)

student: Indicates whether the individual is a student. (Yes, No)

balance: The balance on the individual's credit card.

income: The individual's annual income.

Importing the Dataset

There are a few options to import the dataset. You may use the ISLR packages and load the data directly. You can also find the dataset within our Datasets folder and read it as a .csv file. Below we use the latter option.

# Loading the necessary packages
library(tidyverse)
library(tidymodels)

credit_data <- read.csv('Datasets/Default.csv')
credit_data <- as_tibble(credit_data) %>% rename(default='X...default')

slice_head(credit_data, n = 8)

default	student	balance	income
<chr>	<chr>	<dbl>	<dbl>
No	No	729.5265	44361.625
No	Yes	817.1804	12106.135
No	No	1073.549	31767.139
No	No	529.2506	35704.494
No	No	785.6559	38463.496
No	Yes	919.5885	7491.559
No	No	825.5133	24905.227
No	Yes	808.6675	17600.451

dim(credit_data)

OUTPUT[1] 10000 4

Let's begin by recreating some of the charts for the ISLR book. This is meant to provide additional practice and some thinking around what features are more useful.

library(ggthemr)
library(ggplot2)

# setting the them for visualization
ggthemr('flat')

# setting plot dimensions
options( repr.plot.width = 12, repr.plot.height = 8 )
ggplot(data = credit_data, aes(x = balance, y = income, color = factor(default))) + 
    geom_point() + 
    ggtitle('Scatter Plot of Income vs Balance by Default Status')

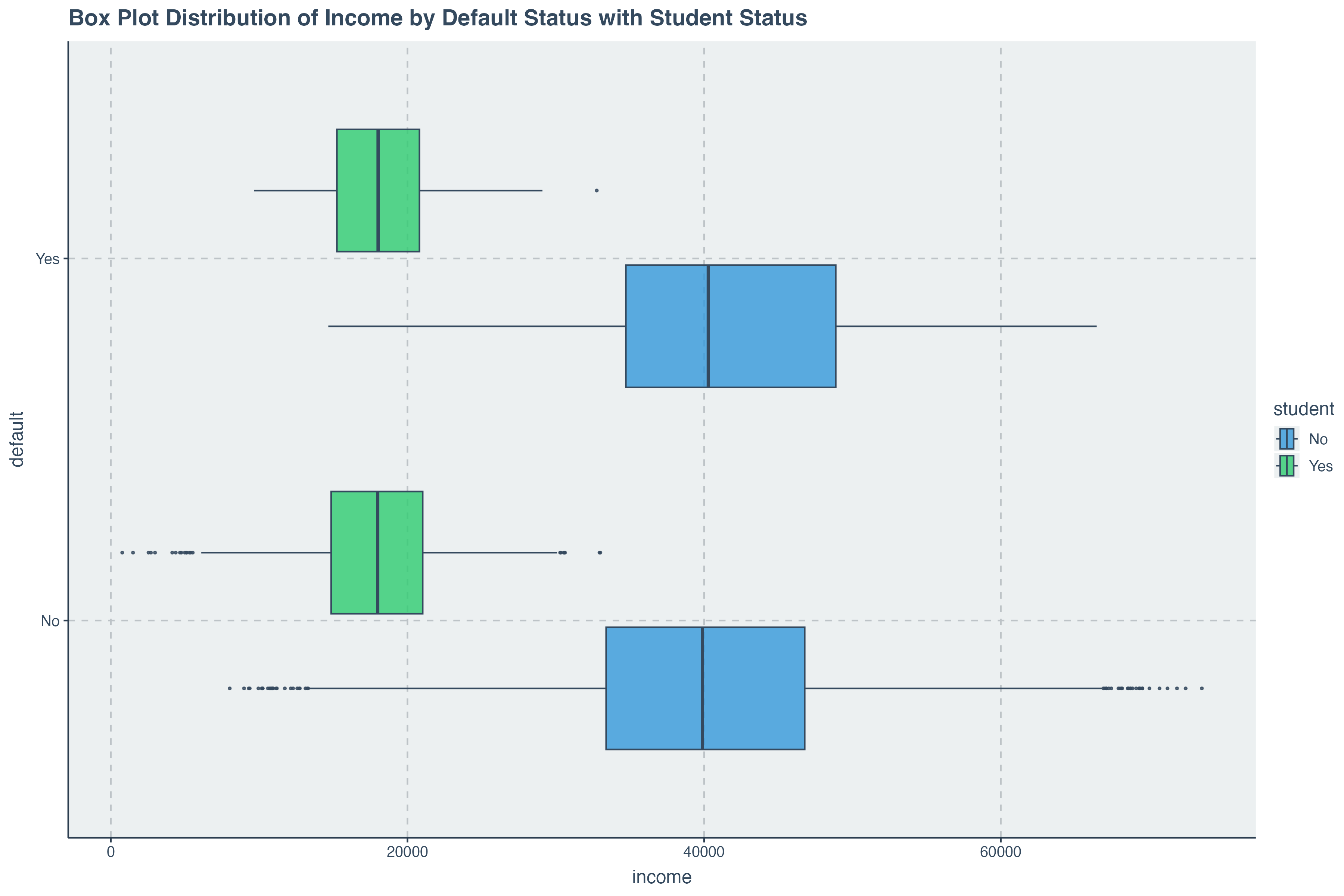
ggplot( data = credit_data, aes(x = balance, y= default,fill = student) ) + 
        geom_boxplot( alpha = .8) + 
        ggtitle('Box Plot Distribution of Balance vs Default by Student Status')

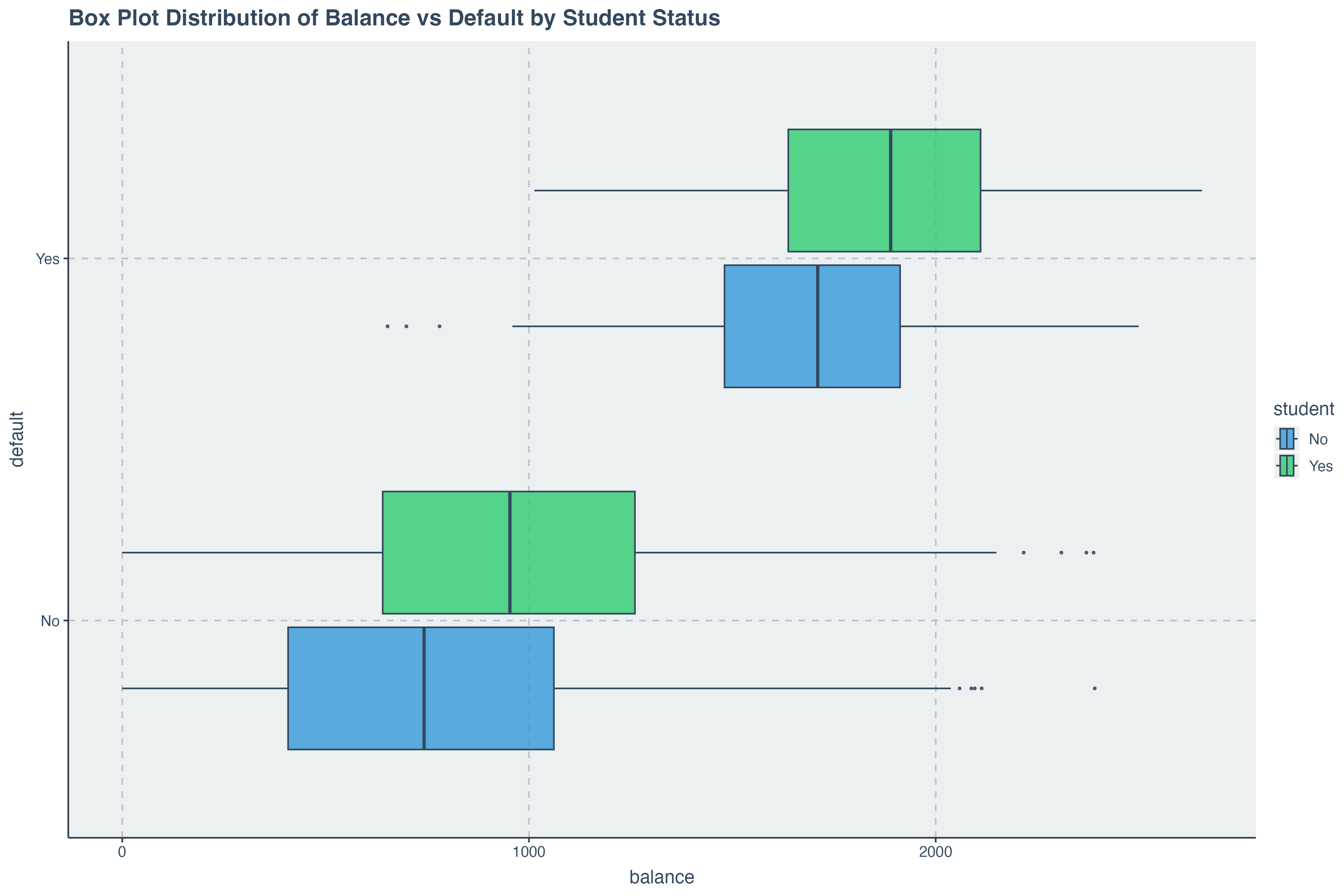
We can begin get an indication that balance offers useful predictive capabilities for determining Default status.

Data Preparation for Modelling

In the previous discussions, we have learned about splitting the dataset ahead of a modeling task. This section covers the preparation we need. Before we split the data, we must convert the default and student into factors inorder to make the eligible as inputs to the model.

Changing Categorical Variables into Factors

# changing categorical variables into factors
credit_data <- credit_data %>%
                mutate( default = as.factor(default),
                        student = as.factor(default))

credit_data %>% head()

Splitting the dataset into Train and Test

We can now go ahead and split the data into train and test groups.

# for reproducibility
set.seed(514)

# setting the split model
data_split = initial_split( credit_data, prop = .8, strata = 'default' )

# splitting the dataset
train_data = training(data_split)
test_data = testing(data_split)

Building the Logistic Regression Model

On this section, we will build a logistic regression model using the tidyverse and tidymodels packages in R. Logistic regression is used to model the probability of a binary outcome based on one or more predictor variables. We will use the Default dataset from the ISLR package to demonstrate this process.

Recall that the model takes the form:

$$p(y = Default | X) = \beta_0 + \beta_1X$$

With the logistic function, it can be written as:

$$ p(Y) = \frac {e^{\beta_0 + \beta_1 X}} {1 + e^{\beta_0 + \beta_1 X} } $$

Now let's see the implementation of this with tidymodels. As usual, with tidymodels, we begin with configurations of the model type, engine and model task.

# Specify a logistic regression model
logistic_model <- logistic_reg() %>%
                   # Set the engine to "glm" which uses the generalized linear model function in R
                   set_engine("glm") %>% 
                   # Set the mode to "classification" since logistic regression is used for binary outcomes
                   set_mode("classification")  

Describing the and Fitting the Model

Our model itself is of the form:

$$ p(x) = \beta_0 + \beta_1 Income + \beta_2 balance $$

Let's run a fit on our model and display the model parameters we have received.

model <- logistic_model %>% 
           fit( data = train_data, formula = default ~ income + balance )

tidy(model)

OUTPUT A tibble: 3 x 5 term estimate std.error statistic p.value (Intercept) -1.159071e+01 4.879481e-01 -23.75398 9.993783e-125 income 2.050130e-05 5.520763e-06 3.71349 2.044203e-04 balance 5.680010e-03 2.539834e-04 22.36370 8.883035e-111

The logistic regression model output is similar to the linear regression, however, it is important to consider the intepretation of the model for the specific task.

Model Parameter Output

We have already seen how to get the model parameters output in tidy format. A useful detail to add here is that we can also retrive the summary of the model which is built into the glm function. The results can then be visualized below:

model %>%  pluck("fit") %>% summary()

OUTPUTCall: stats::glm(formula = default ~ income + balance, family = stats::binomial, data = data) Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -1.159e+01 4.879e-01 -23.754 < 2e-16 *** income 2.050e-05 5.521e-06 3.713 0.000204 *** balance 5.680e-03 2.540e-04 22.364 < 2e-16 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 2394.2 on 7999 degrees of freedom Residual deviance: 1288.3 on 7997 degrees of freedom AIC: 1294.3 Number of Fisher Scoring iterations: 8

Making Predictions with the Trained Model

With our logistic regression model trained, we can now make predictions on the test dataset. It is important to compare the predicted results with our intuition and the actual outcomes to evaluate the model’s performance. The following code snippet demonstrates how to predict the default status of individuals based on their balance and income using the trained model.

OUTPUTA tibble: 6 x 1 .pred_class No No No No No No

We notice that the predictions are already converted into the final factor outcome. This is certainly useful, however, it is important to note that these predictions are converted from probabilities. To get the probabilities, we can run the following code:

predict( model, new_data = test_data, type = 'prob' ) %>% head()

OUTPUTA tibble: 6 x 2 .pred_No .pred_Yes 0.9985540 1.445977e-03 0.9983266 1.673441e-03 0.9992702 7.298345e-04 0.9916813 8.318657e-03 0.9999741 2.592679e-05 0.9994837 5.162513e-04

Now we see that for each prediction, there is a probability associated with the factor value Yes or No

Assessing Model Accuracy

Just like with linear regression, it is crucial to assess the accuracy and performance of our logistic regression model. This helps us understand how well our model is performing and whether it is making accurate predictions. The following steps demonstrate how to evaluate the accuracy of the logistic regression model using various metrics.

augment for combining predictions with test data

The code below then uses the augment function which combines the new_data and predictions of a model into a single tibble object.

augment( model, new_data = test_data ) %>% head()

OUTPUTA tibble: 6 x 7 .pred_class .pred_No .pred_Yes default student balance income No 0.9985540 1.445977e-03 No No 729.5265 44361.63 No 0.9983266 1.673441e-03 No No 825.5133 24905.23 No 0.9992702 7.298345e-04 No No 606.7423 44994.56 No 0.9916813 8.318657e-03 No No 1112.9684 23810.17 No 0.9999741 2.592679e-05 No No 0.0000 50265.31 No 0.9994837 5.162513e-04 No No 485.9369 61566.11

conf_mat returns to us the confusion matrix

We can then pass these directly into a confusion matrix. The confusion matrix gives us a view of what the correct predictions where and the incorrect predictions were as well.

augment( model, new_data = test_data ) %>% 
        conf_mat( truth = default, estimate = .pred_class  )

OUTPUT Truth Prediction No Yes No 1936 40 Yes 6 18

Turning Confunsion Matrix into a Visual

If we wish to do so, we can also that the confusion matrix into a plot directly within the code above by passing the autoplot function and defining the type of plot desired.

augment( model, new_data = test_data ) %>% 
         conf_mat( truth = default, estimate = .pred_class  ) %>%
         autoplot( type = 'heatmap') +
         ggtitle("Confusion Matrix for Logistic Regression Model")

Computing Accuracy Metric

In addition to generating a confusion matrix, we can directly compute the accuracy of our logistic regression model using the accuracy function. Accuracy is a key metric that indicates the proportion of correct predictions made by the model out of all predictions. The following code snippet demonstrates how to compute the accuracy of the model.

augment( model, new_data = test_data ) %>% 
         accuracy( truth = default, estimate = .pred_class ) 

OUTPUTA tibble: 1 x 3 .metric .estimator .estimate accuracy binary 0.977

This multiple logistic regression model with two features is very accurate with a test data accuracy of $97.7%$.

Additional Model Assessment Metrics

While accuracy is a useful metric to understand how well the model is performing, it is not always sufficient, especially when dealing with imbalanced datasets. Other metrics such as sensitivity (recall), specificity, precision, and the F1-score provide a more comprehensive view of the model’s performance. Below, we calculate these additional metrics for our logistic regression model.

augment( model, new_data = test_data ) %>% 
    summarise(
               accuracy = mean( .pred_class == default),
               sensitivity = sens_vec(truth = default, estimate = .pred_class),
               specificity = spec_vec(truth = default, estimate = .pred_class),
               precision = precision_vec(truth = default, estimate = .pred_class),
               recall = recall_vec(truth = default, estimate = .pred_class),
               f1 = f_meas_vec(truth = default, estimate = .pred_class)
            )

OUTPUTA tibble: 1 x 6 accuracy sensitivity specificity precision recall f1 0.977 0.9969104 0.3103448 0.9797571 0.9969104 0.9882593

Turning Confunsion Matrix into a Visual

If we wish to do so, we can also that the confusion matrix into a plot directly within the code above by passing the autoplot function and defining the type of plot desired.

augment( model, new_data = test_data ) %>% 
         conf_mat( truth = default, estimate = .pred_class  ) %>%
         autoplot( type = 'heatmap') +
         ggtitle("Confusion Matrix for Logistic Regression Model")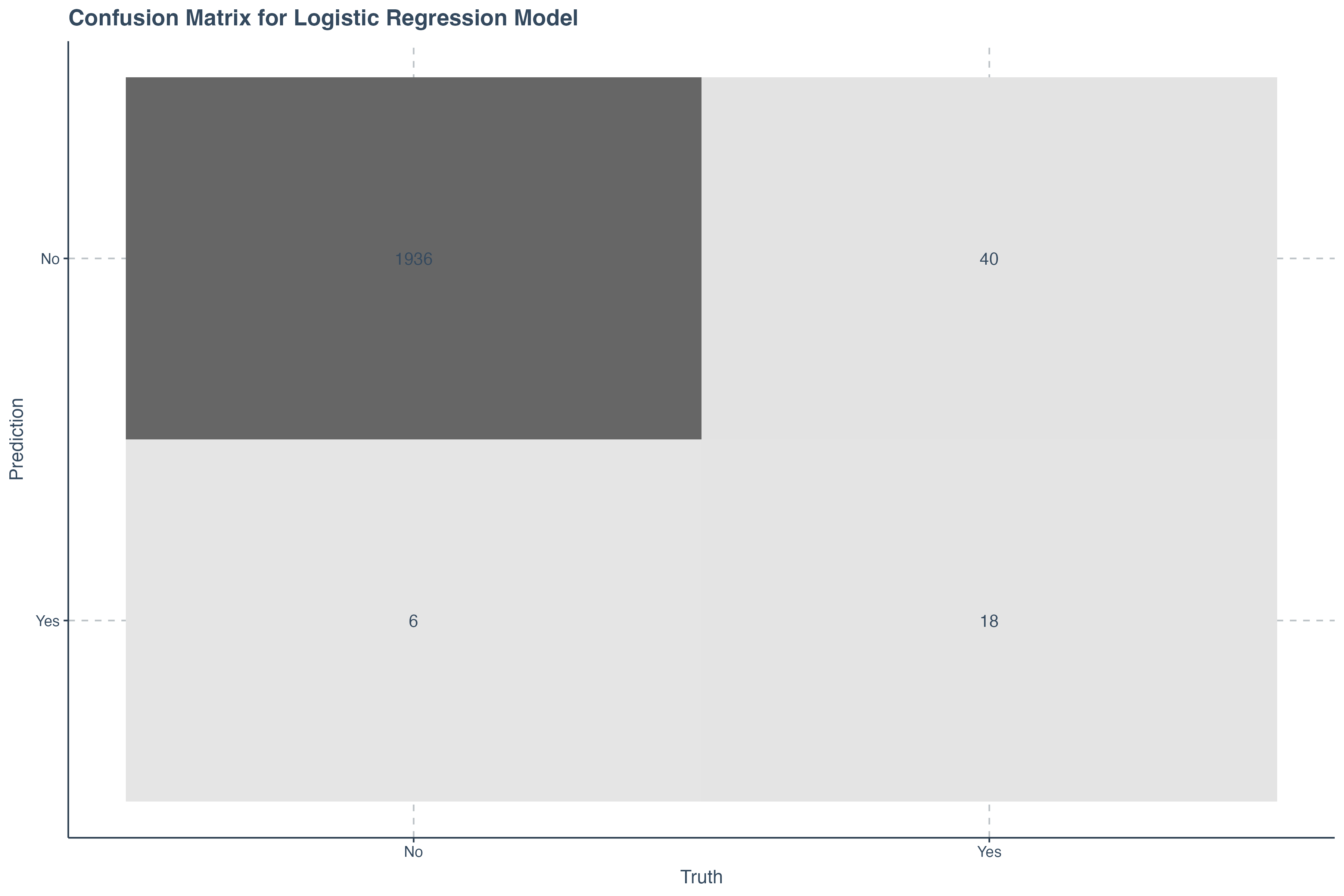

ROC Curve

The Receiver Operating Characteristic (ROC) curve is a graphical representation of a classifier’s performance. It plots the True Positive Rate (Sensitivity) against the False Positive Rate (1 - Specificity) at various threshold settings. The Area Under the ROC Curve (AUC) is a single scalar value that summarizes the performance of the classifier across all thresholds.

Below is a demostration demonstrate how to generate and interpret the ROC curve for our logistic regression model.

augment( model, new_data = test_data ) %>%
    # set probabilities for the "No" class
    roc_curve(truth = default, .pred_No) %>% 
    autoplot() +
    ggtitle("ROC Curve for Model Performance") + theme_minimal()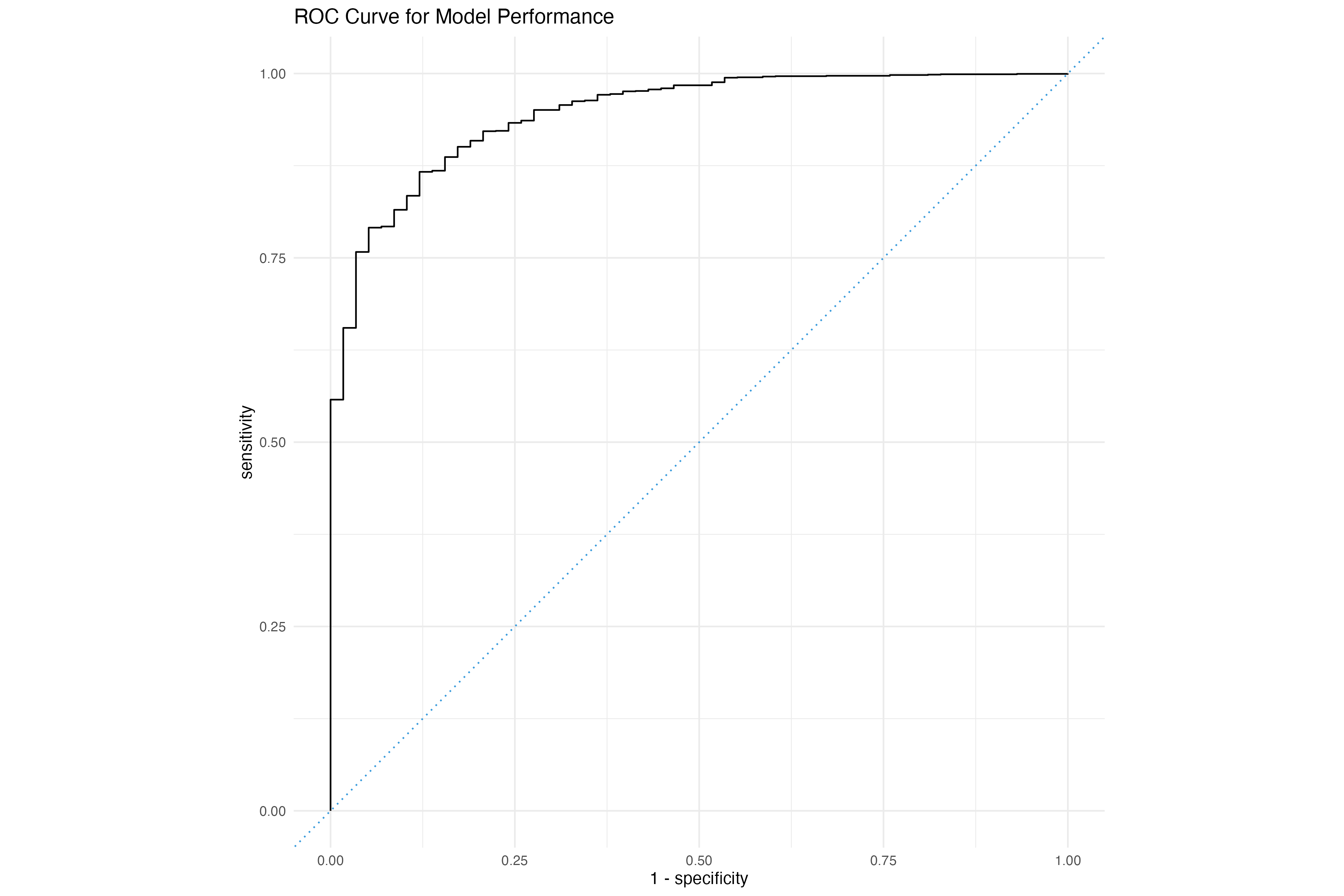

# Calculate AUC
augmented_data <- augment( model, new_data = test_data )
auc_result <- roc_auc(augmented_data, truth = default, .pred_No)

# Display the AUC
print(auc_result)

OUTPUT .metric .estimator .estimate 1 roc_auc binary 0.946

Key Takeaways from the ROC Curve:

• Accuracy: The area under the ROC curve (AUC-ROC) represents the model's overall accuracy. An AUC-ROC of 1 represents a perfect classifier, while an AUC-ROC of 0.5 represents a random classifier.
• True Positives and False Positives: The curve shows the relationship between true positives (correctly classified instances) and false positives (incorrectly classified instances) at different thresholds.
• Threshold Selection: The ROC curve helps in selecting the optimal threshold for the model, which balances the true positive rate and false positive rate.
• Model Comparison: ROC curves can be used to compare the performance of different models, with higher AUC-ROC values indicating better performance.

Interpreting the ROC Curve:

A curve closer to the top-left corner indicates better performance, as it represents a higher true positive rate and a lower false positive rate.

A curve closer to the diagonal line indicates random performance, as it represents an equal true positive rate and false positive rate.